Post

Qwen3 RL Secret

Posted
By 21 min read

GSPO：Qwen3 的 RL 秘方，奖励宜粗不宜细？

Qwen 团队提出了一种名为「[组序列策略优化]（Group Sequence Policy Optimization, GSPO）的新型强化学习算法，尝试解决训练超大规模语言模型时遇到的不稳定和效率低下的问题。

  • 与以往算法（如 [GRPO]在单个 token 层面进行调整不同，GSPO 的核心思想是在整个句子或段落（sequence）的层面上进行评估和优化。
  • 它认为，奖励是给整个回复的，那么模型的更新也应该基于整个回复的表现，而不是拆分到每个词。
  • 论文通过实验证明，GSPO 不仅训练过程更稳定、效率更高，尤其是在训练复杂的混合专家（MoE）模型时表现出色，还简化了训练系统的设计。
  • 这一算法的成功应用，是最新 Qwen3 模型性能显著提升的关键因素之一。

论文： Group Sequence Policy Optimization

一、背景知识：LLM 强化学习

当前主流的 LLM 的训练，基本分为三个步骤：

  1. 预训练：让模型阅读互联网上几乎所有的文本，学会语言的规律和海量的知识。
  2. 监督微调：用高质量的问答数据对模型进行调教，让它学会按指令进行对话。
  3. 强化学习：目标是提升模型的推理、遵循复杂指令等高阶能力。

我们重点关注第三步。目前 LLM 的 RL 阶段，最主流的算法是 PPO（Proximal Policy Optimization） 以及其衍生品。

1.1 PPO：小步快跑，保持稳定

PPO 的核心思想是「小步快跑，保持稳定」。比如一下你在训练一只宠物狗（LLM）：

  • 指令（Prompt）：你对它说「握手」。
  • 动作（Response）：它可能抬起了左脚。
  • 奖励（Reward）：你觉得还不错，给它一个 80 分的奖励。
  • 学习（Optimization）：PPO 算法会微调狗的「大脑」（模型参数），让它下次更有可能做出「抬左脚」这个动作。

为了防止狗一下子学「野」了，做出一些奇怪的动作，PPO 会确保每次更新后的新策略和旧策略不会相差太远。这就是「近端（Proximal）」的含义。

这个过程依赖一个至关重要的数学工具——[重要性采样]（Importance Sampling）。

1.2 重要性采样

在训练中，为了提高效率，我们通常是用「旧模型」生成一大批数据，然后用这批数据来更新「新模型」。这就带来一个问题：用旧模型的数据来指导新模型，会不会有偏差？

会的。重要性采样就是解决这个问题的，它的思想是：我们可以通过给旧的每个数据点乘以一个「权重」，来修正它的代表性，从而估算出当前的情况。

这个权重就是重要性权重（Importance Ratio），它的计算方式很简单：

\[\text{权重} = \frac{\text{某个数据点在「新」分布下出现的概率}}{\text{它在「旧」分布下出现的概率}} = \frac{\pi_{\text{新}}(动作)}{\pi_{\text{旧}}(动作)} \\\]

如果一个动作在新策略下变得更可能出现，它的权重就大于 1，反之小于 1。通过这个权重，PPO 就能利用旧数据安全地更新模型了。

1.3 PPO 的局限

PPO 有一个巨大的实践难题：它需要一个额外的价值模型（Value Model），或者叫 Critic 模型。注意，不要把价值模型和奖励模型弄混淆。价值模型不是提供额外的奖励来源，而是通过学习预测未来的期望回报，提供了一个动态的基准，用来校准 RM 提供的原始奖励信号，生成更稳定、信息量更大的 Advantage 信号，从而稳定并加速 PPO 的训练。

可以参考这篇文章：

目前常见的做法，价值模型会给每一个 token 打分，而且它和策略模型本身一样大，训练它既耗费资源又困难，而且估算往往不准，成为整个系统中最脆弱的一环。

二、前人的做法

2.1 GRPO：用平均分充当基线

为了摆脱昂贵的价值模型，DeepSeek 团队提出了 GRPO（Group Relative Policy Optimization） 算法。

GRPO 的想法是：我不需要一个额外的价值模型来给打一个「绝对分」，而是采样多次，直接用奖励模型的平均值来充当这个「基线」，或者叫「优势」（Advantage）。

具体来说，针对同一个问题，GRPO 让模型生成一组（比如 4 个）不同的回答。然后，一个奖励模型会给这 4 个回答分别打一个总分。

  • 回答 A：95 分
  • 回答 B：70 分
  • 回答 C：85 分
  • 回答 D：80 分

平均分是 82.5 分。那么：

  • 回答 A 的优势（Advantage） 就是正的，因为它高于平均分。
  • 回答 B 的优势就是负的，因为它低于平均分。

这样，GRPO 就巧妙地绕过了价值模型，通过组内排名的相对优势来指导模型学习。对于优势为正的回答，模型会学习增加它出现的概率；对于优势为负的，则降低其概率。

2.2 GRPO 的局限

Qwen 团队指出，GRPO 在应用 PPO 的核心机制——重要性采样时，犯了一个错误：GRPO 在 token 级别计算重要性权重，而不是在整个序列级别。

在数学上，重要性采样理论要求我们对从一个分布中采出的多个样本求平均，才能准确修正分布的偏差。而 GRPO 在每个时间步，只基于一个采样出的词元 $y_t$ 来计算权重，这个权重充满了随机噪声，失去了修正分布的意义。

这种噪声会随着回答的变长而不断累积，最终像滚雪球一样，引发灾难性的模型崩溃。尤其是在训练深度更深、结构更复杂的混合专家（MoE）模型时，这种不稳定性会被急剧放大。

2.3 [路由回放]（Routing Replay）

为了让 GRPO 这类算法能在混合专家（MoE）模型上稳定运行，研究者们采用了一种名为 「路由回放」（Routing Replay） 的策略。

可以将 MoE 模型类比为一个拥有众多专家的咨询公司。每次处理一个词元时，都会由一个「路由网络」指派几位最相关的专家参与计算。问题在于，模型参数稍有更新，这个「指派名单」就可能发生变化，导致前后两次计算缺乏可比性。

「路由回放」的作用：

  • 在模型生成数据时，记录下每个词元由哪些专家处理。
  • 在模型优化、需要进行新旧对比时，强制新模型「回放」这套完全相同的专家指派名单。

尽管有效，但这毕竟是一个额外的「补丁」，增加了系统复杂性，也限制了模型自由探索更优专家组合的能力。而 GSPO 的出现，则从根本上解决了这个问题，让这个补丁变得不再必要。

三、GSPO 的核心机制

GSPO 的核心思想简单而深刻：奖励的单位，应该与优化的单位相匹配。

奖励是给整个回答序列的，那么我们的重要性权重和优化过程，也应该在序列（Sequence） 的层面上进行。这就像老师批改作文，是通读全文后给出一个总分和评语，而不是逐字逐句地打分。

3.1 序列级重要性权重

GSPO 抛弃了 GRPO 的词元级权重，定义了一个全新的序列级重要性权重 $s_i(\theta)$：

$s_i(\theta) = \left( \frac{\pi_\theta(y_ix)}{\pi_{\theta_{old}}(y_ix)} \right)^{\frac{1}{y_i}} \$

其中：

  • $\frac{\pi_\theta(y_ix)}{\pi_{\theta_{old}}(y_ix)}$：这是整个序列 $y_i$ 在新旧策略下的概率比。它直观地反映了：对于旧模型生成的这个回答，我们的新模型是更「喜欢」它了（概率变高），还是更「讨厌」它了（概率变低）。这才是对重要性采样的正确应用。
  • $(\cdot)^{\frac{1}{y_i}}$：代表对序列长度 $y_i$ 开方，相当于取几何平均值。

为什么要取几何平均？

一个句子的概率是所有词元概率的连乘积。一个长句子的概率会是一个极小的数（比如 $10^{-100}$）。如果不做处理，长短句的权重会天差地别，导致数值计算极其不稳定。

取几何平均，就好像把整个句子的「权重增益」平均分配到每个词元上，将重要性权重拉回到一个合理的、可比较的范围（比如 [0.5, 2.0]）。这增强了算法的稳定性和鲁棒性。

3.2 梯度对比：GSPO 为何更稳定？

我们可以通过对比梯度更新的「指挥信号」来理解两者的差异：

  • GRPO 的指挥信号：对于一个好回答，它会对里面的每个词说：A词，你很重要，给你1.2倍的权重去学习！B词，你一般般，给你0.9倍的权重…… 这些权重充满噪声，指令互相矛盾，模型学起来晕头转向。
  • GSPO 的指挥信号：对于一个好回答，它会先给出一个总体的评价，比如 这个回答整体不错，权重是1.1，然后对里面的所有词说：大家是一个团队，都朝着这个1.1倍权重的方调整。

四、实验效果

Qwen 团队在 MoE 模型（Qwen3-30B-A3B-Base）和复杂的数学、编程任务上对 GSPO 和 GRPO 进行了对比。

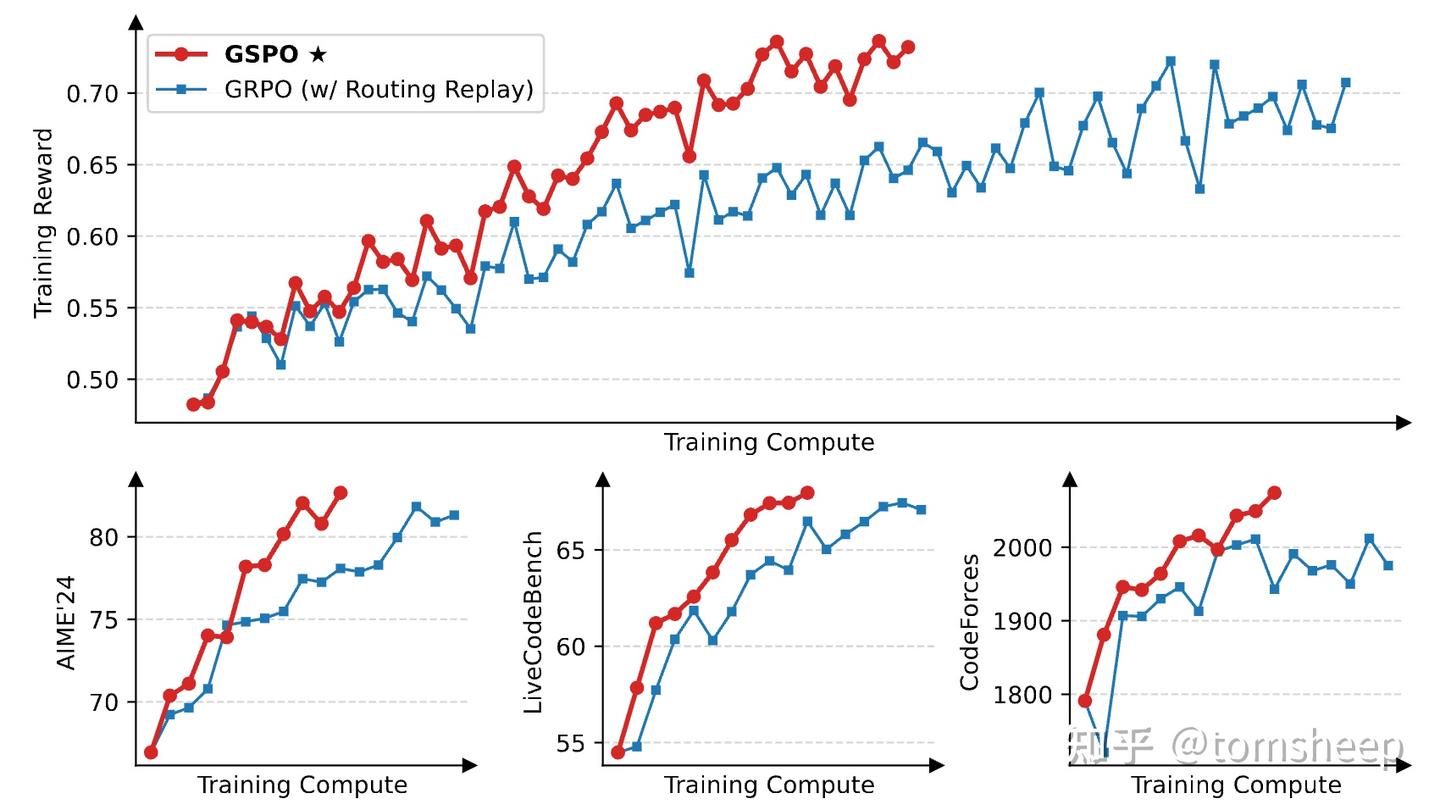
4.1 发现一：更稳、更快、更强

在相同计算资源下，GSPO 在训练奖励和下游任务性能上，都稳定且持续地优于 GRPO。

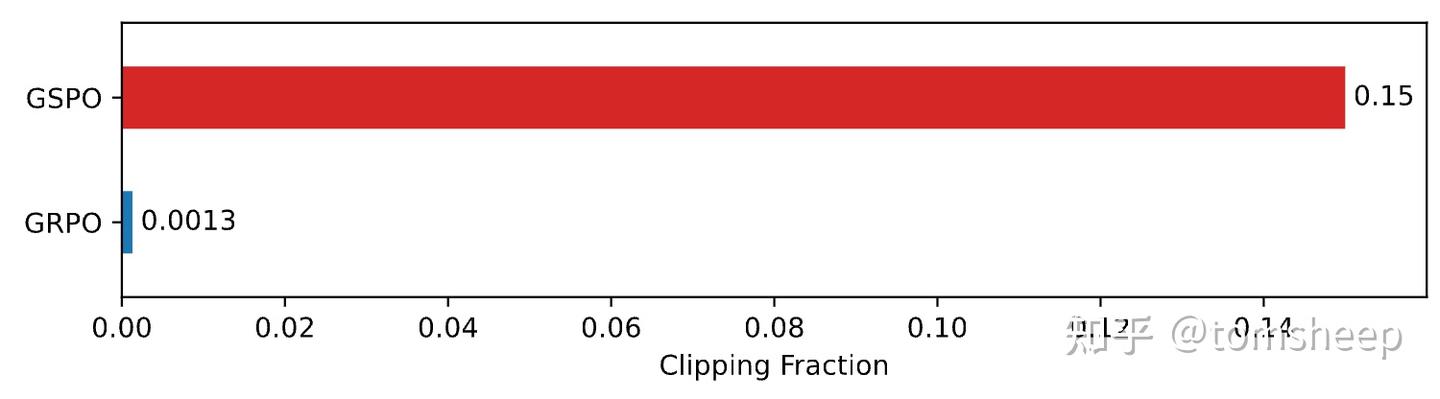
4.2 发现二：反直觉的「裁剪悖论」

PPO 类算法都有一个「裁剪（clipping）」机制，用于丢弃那些与当前模型偏差太大的样本。实验中出现了一个非常反直觉的现象：

GSPO 裁剪掉的词元比例远高于 GRPO，两者相差近两个数量级。这听起来是不是很奇怪？丢弃了更多的数据，学习效果反而更好？

可以这样理解：

  • GRPO 的策略：像一个新手投资者，分析了 1000 个项目，觉得每个都沾点边，于是给每个都投了点钱。结果是，大部分投资的微小收益被少数的巨大亏损所抵消，整体回报率很低。它利用了所有数据，但这些数据充满了噪声。
  • GSPO 的策略：像一个经验丰富的投资大师，同样分析了 1000 个项目，但它有极其严格的筛选标准（序列级裁剪）。最终，它只挑选了 50 个最优质的项目进行重仓。虽然它「浪费」了研究另外 950 个项目的时间，但这 50 笔高质量的投资带来了惊人的回报。

GSPO 的成功告诉我们：在强化学习中，学习信号的质量远比数量重要。 通过严格的序列级筛选，GSPO 确保了每一次模型更新都来自于「高信噪比」的优质样本，因此学习过程更高效、方向更正确。

4.3 发现三：MoE 上的有效性

混合专家（MoE）模型是当前大模型发展的前沿方向，它通过稀疏激活部分网络来节省计算，但这也给 RL 训练带来了独特的稳定性挑战。

  • MoE 的困境：在 MoE 模型中，参数更新后，对于同一个输入，被激活的「专家」网络可能会发生变化。
  • GRPO：这对于 GRPO 是致命的。它的词元级权重 $\frac{\pi_{\text{新}}(y_t…)}{\pi_{\text{旧}}(y_t…)}$ 的分子和分母可能是由完全不同的子网络计算出来的，比较它们毫无意义，导致权重剧烈波动。为了解决这个问题，研究者们不得不设计复杂的「路由回放（Routing Replay）」策略，增加了系统的复杂度和开销。
  • GSPO：GSPO 则完全没有这个烦恼。因为它关注的是宏观的、整个序列的概率，这个指标对于底层具体的专家组合变化不那么敏感。就像一家大公司的 CEO，他关心的是公司本季度的总体财报（序列概率），而不是某个具体部门的人员微调（专家路由变化）。

实验证明，GSPO 无需任何额外技巧，就能稳定地训练 MoE 模型，大大简化了训练流程。

五、总结

5.1 贡献

  • 理论创新：明确指出 GRPO 等算法在词元级重要性采样上的理论缺陷，提出优化单位应与奖励单位（序列）一致，回归重要性采样的正确用法。
  • 算法提升：提出 GSPO 新算法，通过序列级权重计算和裁剪，显著提升训练稳定性、收敛效率和最终性能，并用长度归一化（几何平均）解决不同长度序列的数值稳定问题。
  • 工程简化：彻底解决 MoE 训练不稳定问题，移除对「路由回放」等复杂技巧的依赖，简化 RL 训练流程，并提升对数值精度差异的容忍度，降低工程复杂度。
  • 实际验证：GSPO 已在 Qwen3 等大规模模型中成功应用，展现出工业级的有效性和可靠性。

5.2 局限

  • 粗粒度奖励：GSPO 只对整个序列赋予单一奖励，无法区分长回复中的优劣部分，可能导致学习效率不高。
  • 仍然依赖奖励模型：性能高度依赖奖励模型的质量，若奖励模型有偏见或缺陷，GSPO 会放大这些问题。
  • 场景适用性：在需要词元级反馈的任务（如代码调试）中，GSPO 的「一刀切」优化方式可能不如细粒度方法。
  • 实验范围有限：目前实验主要集中在数学和编程等推理任务，对开放性、主观性强的领域（如创意写作、情感对话）效果尚需进一步验证。
Generative AI, Artificial Intelligence
Algorithm
This post is licensed under CC BY 4.0 by the author.