「Paper Reading」 LLM RLHF 2024论文(三十九)FoT
【论文解读】rStar-Math:无需蒸馏,小模型左脚踩右脚螺旋升天
伪代码实现
微软在[SLM]小模型领域真的有一手,刚看到MSRA公布的一篇新(2025年1月)论文,用MCTS + 步骤级别的[Reward Model](也基于SLM) 让小语言模型的推理性能大幅提升,而且这个过程还能顺便起到「数据增强」的效果,反过来再训练策略模型与奖励模型,实现自我进化(self-evolution)。
论文:[2501.04519] rStar-Math: Small LLMs Can Master Math Reasoning with Self-Evolved Deep Thinking
主要内容
1.作者和团队信息
- 这篇论文是由来自微软亚洲研究院(Microsoft Research Asia)的研究团队完成,作者列表包括 Xinyu Guan、LiLyna Zhang、Yifei Liu、Ning Shang、Youran Sun、Yi Zhu 等人,涵盖了多位在大模型、高级算法以及自动推理领域富有经验的研究者。
- 团队在小型语言模型(SLM)方面进行了大规模的数学推理研究,并在开源社区(如 GitHub)分享了相关代码和数据。值得注意的是,微软亚洲研究院在自然语言处理、语音识别、图像处理等多个领域长期处于国际领先地位,对大规模预训练模型、自动推理和数学问题求解均有丰富的探索。
2.背景和动机
- 时间:论文于 2025 年 1月公布在arxiv上。
- 目的:研究如何让小模型(小于 10B 级别)在数学推理方面达到甚至超越现有的较大模型或商业化模型(如OpenAI o1)。
背景:
- 传统上,大语言模型在数学推理时往往缺乏「一步步严谨验证」的能力,通常以单次前向推理(类似 System 1)输出整条答案。这样做速度快,但错误率也高。
- 近年来,越来越多的研究表明,通过在推理时增加「深度思考(System 2)」环节,可以显著提升模型在解决复杂推理任务的正确率。
- 本文的核心动机就在于:能否让小模型(SLM)也具备深度思考、迭代性的多步推理能力,从而在不依赖更强教师模型的前提下,依靠自身迭代训练来获得高性能的数学推理能力。
3.相关研究
- 在过去,许多研究利用 GPT-4 或其他强大模型进行「教师-学生」风格的知识蒸馏(distillation),为较小模型生成大规模的数学题和解答数据。
- 然而,这类方法受限于教师模型的能力:如果教师模型在某些高难度问题上本身就不行,那么小模型也无法收到高质量的解题示例。
- 此外,大模型在生成完整解题过程时,也很可能出现错误中间步骤但最终碰巧得到正确答案,或完全错误无法检测的问题。
- 为了解决这些难点,近年来的研究开始尝试在「测试阶段」进行多次采样、增加搜索树、或者由奖励模型筛选最高分解答,但这对于开源小模型的效果仍然不够明显。
4.核心思路
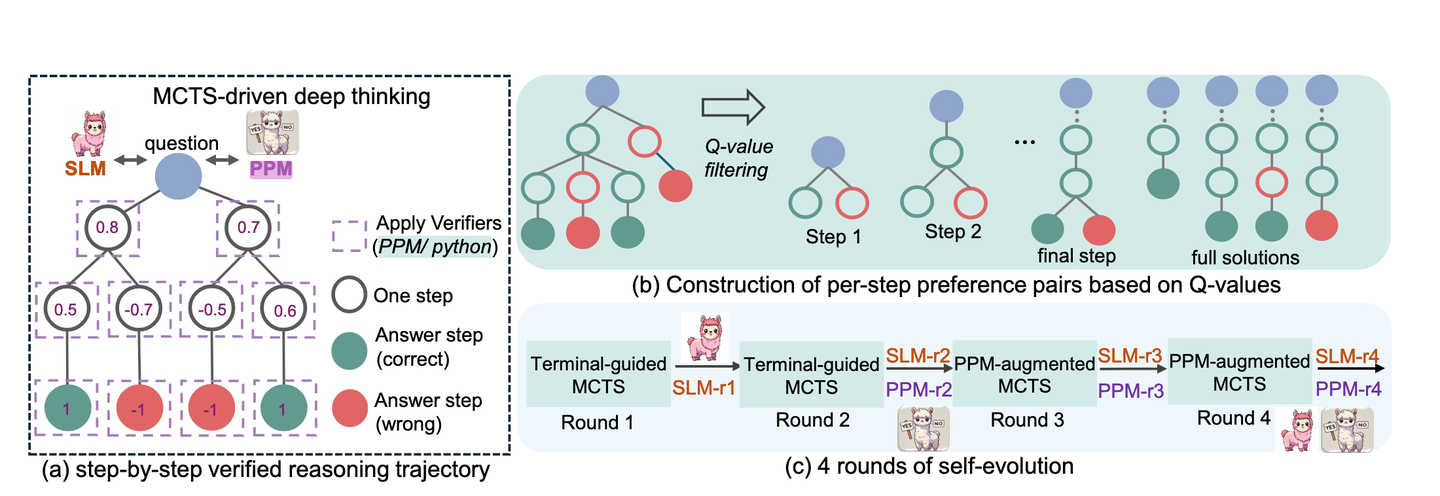
论文提出了一个名为「rStar-Math」的方法,让小模型模拟人类在高难度数学竞赛推理时的做法,以「深度思考」的方式反复搜寻可能的推理路径。其核心思路包括:
- 使用小型语言模型作为「策略模型(policy model)」在多步推理中提供候选步骤。
- 利用一个同样由小模型训练而成的「过程奖励模型(process reward model, PRM)」来对每一步的推理质量打分,从而在多次蒙特卡洛树搜索(MCTS)中筛选出最有潜力的节点。
- 从这些多次搜索生成的轨迹中,选取「每一步都被验证过」的正确中间步骤及最终正确答案,形成高质量的训练数据,反过来再训练策略模型与奖励模型,实现自我进化(self-evolution)。
5.方案与技术
论文的具体技术方案可以分解为:
- Monte Carlo Tree Search(MCTS):将数学题的解题过程拆分为多步动作搜索,每一步动作是产出一个、含有相应 Python 代码可执行的中间推理。对于能够通过代码校验或运行成功的步骤才予以保留。
- 代码增强的 CoT 数据合成:在推理路径中强制模型给出 Python 代码并执行,确保每个中间步骤(如代数变换、方程求解)真正可行。最后得到带有「步骤级别」Q 值标注的推理轨迹。
- 过程偏好模型(PPM)训练:为解决「Q 值在步骤层面不够精细」的问题,作者引入正负样本配对的方式(pairwise preference),只要能把「更好步骤」和「更差步骤」区分开就足够训练出一个好的 PPM。它不需要「精确的数字评分」,只需要知道在同样前提下,哪个中间步骤更可能走向正确解答。
- 四轮自我进化(Self-Evolution):先用开源的大模型(如 [DeepSeek-Coder-Instruct]进行初始单轮推理生成数据,然后基于自己训练出的 7B 模型反复堆叠增强,每轮在 MCTS 中取得更优质的数据,用于 SFT(监督微调)策略模型和更新 PPM,从而让小模型在持续迭代中解决更多困难问题。
6.实验与结论
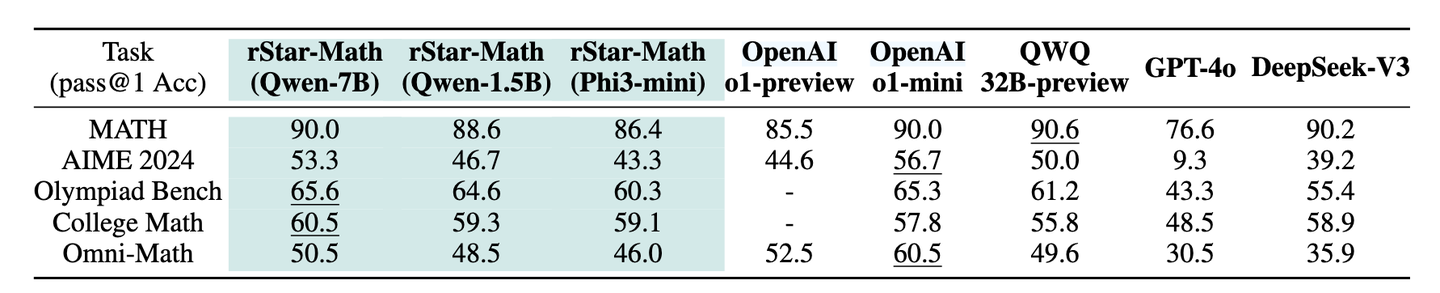
作者在多项数学竞赛与高难度数据集(MATH、[AIME]、[AMC]、Olympiad Bench 等)上进行实验,主要结论包括:
- 对于 7B 级别的 [Qwen2.5-Math] 模型,通过四轮自我进化,rStar-Math 在 MATH 基准上从 58.8% 提升到 90.0%,超过了 OpenAI o1-preview,且逼近甚至匹敌 o1-mini 的 90%。
- 在 AIME 2024 测试上平均能正确解出 15 题中约 8 题,约占 53.3%,高于众多开源模型,成绩相当于美国高中生中前 20% 的水平。
- rStar-Math 在做深度推理时出现了有趣的「自我反思」过程,即若之前步骤出错,后续会有分支回退并切换到更优思路,从而改正错误。
- 通用性测试表明,rStar-Math 也能够在 College Math、GSM8K、GaokaoEn 2023(中国高考英语卷数学子题)等多种数据集上取得显著性能提升。
7.贡献
- 提出了面向小模型的自我进化思路:以往大多使用 GPT-4 之类的大模型提供教师示例,本研究则证明小模型也可「自给自足」,不依赖更强模型进行蒸馏。
- 实现了基于 MCTS 的步骤级别验证:借助代码执行和多次回溯,使得中间推理不再「虚幻生成」而难以检测。
- 创新的过程偏好模型(PPM):针对数学推理的特点,放弃了精确打分,改为偏好对比,使得模型无需人类细粒度标注就能获得细步监督。
- 对后续研究的启示:从理论与工程上扩大了小模型在高难度推理问题上的新可能性,也为其他领域的「自洽式数据生成」提供思路。
8.不足
- 对极高难度或含图像信息的题目仍存在局限:如 AIME 中带有复杂几何示意图的部分题目,rStar-Math 尚不能完全理解图形本身。
- 大量算力和推理时间消耗:虽然单轮 MCTS 依赖 7B 模型并不算过大,但为了生成数十万题的所有多步推理,当轮次增加时,依然需要极大规模的计算资源。
- 依赖能执行的 Python 代码:部分复杂推理(如纯证明题、几何构造等)可能无法单靠 Python 代码判断正确性,还需要其他更复杂的验证机制。
- 覆盖面与问题类型:主要聚焦在中高级别的竞赛数学,尚未在自然语言推理、代码调试等更广泛领域深入验证。
QA
Q1:为什么要使用 MCTS(蒙特卡洛树搜索)而不是简单的多次采样呢?
MCTS 不仅是简单的多次随机采样,还会对生成的中间状态进行「回溯和更新」。在多次搜索迭代中,成功抵达正确答案的分支会获得更高的 Q 值或评分,失败分支则受到惩罚,从而逐渐「引导」模型往更正确的方向采样。这比单纯多次采样加投票更精细,也更类似于人类解题时的「试错与修正」过程。
Q2:论文中多次提到「在步骤级别进行验证」有多重要?
在数学推理中,一个看似正确的结论可能是「歪打正着」:中途若有错误步骤也可能勉强得到正确最终答案。若只看最终答案做筛选,数据中会混入许多不可靠的中间推导。步骤级别验证意味着每一小步都要通过 Python 代码执行来保证合法性,如计算、方程求解等,这会明显减少中间步骤的错误传递,使最后得到的训练数据可靠性更高。
Q3:PPM(过程偏好模型)怎么训练?它和常见的 Reward Model 有什么区别?
一般的 Reward Model(Outcome Reward Model)只在末尾根据答案对错给出一个分值,无法评判中间步骤。PPM 则会在每一步都做打分,对每一个中间步骤给出「好 or 差」的偏好比较。训练时不需要给每一步精确分数,只要从同一「前提状态」中选出更好和更差的步骤,用配对排序的损失函数(pairwise ranking loss)来区分就行。如此就回避了「如何给错误步骤打具体分数」的难题。
Q4:论文指出在多次迭代下会出现「自我反思」现象,这究竟是怎么实现的?
这是在多次搜索和更新过程中自发出现的。因为在 MCTS 不同分支里,如果最初思路出错,奖励估值会降低,下次采样时就会倾向改用其它分支。看上去就像模型自己会「回头纠错」。这种自我反思并非额外编写的「prompt」或「模板」去告诉模型怎么反思,而是深度搜索与奖励反馈的自然结果。
Q5:这项方法是否能够适用于其他领域,比如写代码、通用的逻辑推理?
作者在论文中也讨论了这一点:关键在于是否能对「中间步骤」进行可靠验证。如果是代码场景,可以通过多组运行测试(test cases)来验证中间过程是否正确;如果是更一般的常识推理,可能需要专门的知识库或人类标注的反馈。只要有办法为每个中间过程建立「充分的可行性测试」,都可以借鉴文中「小模型-搜索-奖励」的自进化思路。
Q6:如果我想在自己的项目中尝试 rStar-Math,应该注意哪些工程细节?
- 算力需求:即便是 7B 模型,也要进行大量 MCTS 搜索,对硬件资源是个考验。
- 代码执行环境:要确保每一步生成的 Python 代码能正确在沙箱或独立环境里运行,以防止安全风险。
- 数据质量:如果题库本身存在错误答案或者超出模型能力范围,可能会导致训练数据的噪声较多。
- 迭代轮次:论文里跑了四轮,拿到不错的收敛效果。轮次再多虽然更细致,但代价也会更大,需要取平衡。
Q7:如何避免重复验证成本过高?
论文中也提到可以用一些技巧来减少无谓 search,比如使用 PPM 先给出初步评分,优先探索高评分分支;或对已收敛的子树做缓存,避免重复计算。当然,这些工程优化要结合题目规模和硬件情况实际来做。
伪代码实现
下面给出一个「玩具版」的 Python 代码示例,用于演示 rStar-Math 的核心流程:
- 使用蒙特卡洛树搜索 (MCTS) 将一道数学题的求解过程拆分为多步动作,并在每一步产出可以执行的 Python 代码。
- 代码执行成功才保留对应节点,自动赋予步骤级别的 Q 值。
- 用简单的「过程偏好模型 (PPM)」思路进行训练:只做正负样本的对比,无需精准打分。
- 通过多轮自举 (self-evolution) 循环更新策略模型与 PPM。
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
rStar-Math 核心流程示例 (简化版)
演示如何使用:
1)MCTS + 代码执行
2)步骤级别Q值标注
3)过程偏好模型辅助搜索
4)多轮自举迭代
说明:
- 本示例使用一个“玩具”数学任务作为环境: 给出 x^2 = 9, 求解 x=3。
- policy_model() 与 ppm_model() 均为伪模型,用随机/规则的方式来输出候选步骤/打分,仅为演示结构。
- 在真实场景中,需要将 policy_model() 替换为真正的大语言模型调用(例如通过 API 生成代码+CoT),
并在 ppm_model() 中加载/训练一个实际的 Transformer 结构(如 7B)用于过程偏好打分。
- 同理, self_evolution_round() 的迭代也只做了简化演示,实际中会处理大规模数据训练并更新模型权重。
"""
import random
import copy
import numpy as np
# ------------------------ 【玩具环境定义】---------------------------
# 假设我们要解方程 x^2 = 9, 真正想要的答案是 x=3
# 这里把“完成解答”看作找到 x=3 即可, 并在“终端节点打分”时判断是否正确
def check_final_answer(answer: float) -> bool:
"""判断最终答案是否是我们期望的 3(简化示例)"""
return abs(answer - 3.0) < 1e-6
# ------------------------ 【节点类定义】----------------------------
class MCTSNode:
"""
MCTS搜索节点, 维护:
- state: 当前已经生成的(文本,代码)轨迹
- total_q: Q值之和(用于更新平均Q)
- visits: 访问次数
- children: 子节点列表
- parent: 父节点
- code_str: 当前这一步产出的python代码
- step_score: 当前这一步的PPM打分(初始为0)
"""
def __init__(self, state, parent=None):
self.state = copy.deepcopy(state) # state可包含(已生成的步骤,执行上下文等)
self.parent = parent
self.children = []
self.total_q = 0.0
self.visits = 0
self.step_score = 0.0 # PPM给该节点的打分
self.code_str = "" # 该节点所产生的代码(一步)
@property
def avg_q(self):
return self.total_q / self.visits if self.visits > 0 else 0.0
# ------------------------ 【简单的 policy_model】-------------------
def policy_model(current_state: dict) -> str:
"""
伪“策略模型”,输入当前解题上下文,输出下一步(含代码)字符串
在真正的 rStar-Math 里,可替换成一个语言模型, 例如:
prompt = build_prompt(current_state)
code_cot = call_LLM(prompt)
这里仅用随机demo:
1. 有小概率直接给出“x=3”
2. 有小概率给出“x=随机值”
3. 有时生成“中间过程1:设x=2;2^2=4...”
"""
# 模拟几种不同策略:
r = random.random()
if r < 0.3:
# 30% 概率直接输出一个结果
result = random.choice([3.0, -3.0, 2.5, 12.0])
code_str = f"""
# 直接给出猜测的x值
x = {result}
"""
else:
# 70% 概率做“中间步骤”, 再往后推进
step_val = random.randint(1, 5)
code_str = f"""
# 尝试一步运算:例如给x加1
x = {current_state.get('x', 0)} + {step_val}
"""
return code_str
# ------------------------ 【执行代码】-------------------------------
def safe_python_exec(code_str: str, env: dict) -> bool:
"""
安全执行python代码, 成功执行则返回 True; 否则返回 False.
env是执行上下文, 用来存/取变量, 例如 x
这里为了安全仅允许exec简单运算, 不允许import
"""
# 简化实现:若包含import等敏感操作,则判定失败
if 'import' in code_str.lower():
return False
test_env = copy.deepcopy(env)
try:
exec(code_str, {}, test_env)
except Exception:
return False
# 如果执行成功, 把test_env合并回env
env.update(test_env)
return True
# ------------------------ 【简单PPM模型】---------------------------
def ppm_model(partial_state: dict, code_str: str) -> float:
"""
伪 过程偏好模型(只做评分), 在真正的实现中则是一个基于LLM微调的模型.
这里根据是否能让 x 靠近 3 来给一个打分, 范围 -1 ~ 1
"""
# 先尝试执行这段代码, 看看执行后 x 距离3有多远
tmp_env = copy.deepcopy(partial_state)
ok = safe_python_exec(code_str, tmp_env)
if not ok:
return -0.8 # 执行失败, 视为非常负面
# 算一下修改后的 x 距离3
val = tmp_env.get('x', 0)
dist = abs(val - 3)
# 距离越近, 分数越高. 如果恰好=3, 则给最高1.0
score = 1.0 - dist
if score < -1.0:
score = -1.0
if score > 1.0:
score = 1.0
return float(score)
# ------------------------ 【MCTS 核心流程】-------------------------
def mcts_rollout(root: MCTSNode, max_depth=5, c_ucb=1.4) -> None:
"""
对某个根节点做一次MCTS搜索(从根到叶子).
max_depth: 最大深度
c_ucb: UCB探索常数
"""
# 1) Selection
node = root
depth = 0
while node.children and depth < max_depth:
# 基于UCB从 children 选一个
best_ucb = -999999
best_child = None
for ch in node.children:
# UCB = Q + c*sqrt( log(N_parent)/N_child )
ucb = ch.avg_q + c_ucb * np.sqrt(np.log(node.visits+1)/(ch.visits+1e-6))
if ucb > best_ucb:
best_ucb = ucb
best_child = ch
node = best_child
depth += 1
# 2) Expansion: 若还没到max_depth, 则扩展新的子节点
if depth < max_depth:
# 调用策略模型, 生成若干候选
candidates = []
for _ in range(3): # 每步生成3个候选子节点做演示
code_str = policy_model(node.state)
# 先尝试执行, 若执行都失败, 就不扩展
tmp_state = copy.deepcopy(node.state)
ok = safe_python_exec(code_str, tmp_state)
if ok:
# 可扩展
child_node = MCTSNode(tmp_state, parent=node)
child_node.code_str = code_str
node.children.append(child_node)
candidates.append(child_node)
# 在本示例中,不额外做rollout(即simulation), 仅依赖step打分 + 终端判断
# 这里绝大多数纯MCTS会做一个随机rollout到终局, 然后回传reward
# 为简洁省略.
if not candidates:
# 没有可扩展节点,则算叶子节点
pass
else:
# 选第一个candidate作为“leaf”
node = candidates[0]
# 3) Evaluate leaf node reward(简化:如果 x=3则 reward=1,否则0)
terminal_reward = 0.0
final_x = node.state.get('x', 0)
if check_final_answer(final_x):
terminal_reward = 1.0
# 4) Backprop: 回溯更新
# 同时也将PPM给每个节点的step打分加进来(作为更细粒度信息)
current = node
while current is not None:
current.visits += 1
# 叠加PPM打分 + 最终reward
step_r = ppm_model(current.parent.state if current.parent else {}, current.code_str)
current.step_score = step_r
# Q值 = PPM打分 + 最终是否正确(这里只是简单线性和)
q_val = step_r + terminal_reward
current.total_q += q_val
current = current.parent
# ------------------------ 【收集轨迹】-----------------------------
def collect_trajectories(root: MCTSNode, depth_limit=5):
"""
从搜索树中收集所有从根到叶或到达depth_limit的轨迹,
并输出如[(step_code, step_q), ...]的步骤列表
"""
all_paths = []
stack = [(root, [])]
while stack:
node, path = stack.pop()
current_path = path + [(node.code_str, node.avg_q, node.step_score)]
if not node.children or len(current_path) >= depth_limit+1:
# 到达叶子节点 或 达到最大深度
all_paths.append(current_path)
else:
for c in node.children:
stack.append((c, current_path))
return all_paths
# ------------------------ 【PPM训练示例】---------------------------
def train_ppm_with_pairs(trajectories):
"""
简化的过程偏好模型训练示例:
- trajectories: List[List[(code_str, avg_q, step_score)]]
- 我们把 avg_q 最高的当“正样本”,最低的当“负样本”
- 这里不做真正的神经网络训练, 仅打印演示
"""
# 收集所有step
all_steps = []
for path in trajectories:
for (code_str, avg_q, step_score) in path:
# 过滤掉空code
if code_str.strip():
all_steps.append((code_str, avg_q, step_score))
if not all_steps:
return
# 排序
sorted_steps = sorted(all_steps, key=lambda x: x[1], reverse=True)
top2 = sorted_steps[:2] # 最好的2个
bot2 = sorted_steps[-2:] # 最差的2个
print("======== 过程偏好模型(PPM) 训练数据示例 ========")
for i,(cs,aq,st) in enumerate(top2):
print(f"[POSITIVE-{i}] code:\n{cs.strip()}\n => avg_q={aq:.3f}, step_score={st:.3f}")
for i,(cs,aq,st) in enumerate(bot2):
print(f"[NEGATIVE-{i}] code:\n{cs.strip()}\n => avg_q={aq:.3f}, step_score={st:.3f}")
print("============================================\n")
# 真实中: 使用这些正负对来做 pairwise ranking loss 等。
# ------------------------【多轮自举(Self-Evolution)示例】-------------
def self_evolution_round(round_idx: int):
"""
演示单轮自举:
1) 用当前的“policy模型”+“PPM模型”构建的 MCTS搜集数据
2) 生成轨迹, 训练(或更新)policy与PPM
3) 返回新的policy(在此演示中只是打印,不实际更新代码)
"""
print(f"\n===== 第 {round_idx} 轮: MCTS 搜索并生成数据 =====")
# 初始化根节点, state里模拟 x=0 起点
root = MCTSNode({"x": 0.0})
# 做若干次rollout
for _ in range(10): # 这里做10次rollout
mcts_rollout(root, max_depth=5, c_ucb=1.4)
# 收集轨迹
all_paths = collect_trajectories(root, depth_limit=5)
print(f"本轮共得到轨迹数: {len(all_paths)}")
# 打印其中一条轨迹示例
if all_paths:
example_path = random.choice(all_paths)
print("随机展示一条轨迹:")
for step_code, avg_q, step_scr in example_path:
print(f" code={step_code.strip()[:30]}..., avg_q={avg_q:.2f}, step_score={step_scr:.2f}")
# 训练PPM(简化: 仅示例pairwise构造)
train_ppm_with_pairs(all_paths)
# 真实场景中这里应该:
# 1) 选取高Q值正确解的完整轨迹形成监督数据 -> 微调 policy模型
# 2) 提取正负样本对 -> 微调 PPM
# 在这里仅做打印演示, 不做真正update
print(f"第 {round_idx} 轮结束. (玩具示例, 未实际更新 policy/PPM)")
def main():
# 演示跑 2~3 轮, 说明核心思路
for r in range(1, 4):
self_evolution_round(r)
if __name__ == "__main__":
main()